Introduction

PointNet is a clever deep learning approach for understanding 3D geometric data, like point clouds. Unlike other methods that transform data into regular grids or images, PointNet directly processes point clouds, respecting their irregular nature. It’s a simple yet powerful neural network that handles tasks such as object classification and part segmentation efficiently. The key is using a symmetric function, max pooling, which helps the network select important points in the cloud. It’s not just fast; it’s also robust to changes in input points. The project includes a theoretical analysis, showing PointNet’s ability to approximate various functions, and an experimental evaluation, demonstrating its speed and competitive performance compared to other approaches. The contribution lies in designing a deep net architecture for unordered 3D point sets, showcasing its effectiveness in multiple tasks, and providing insights into its stability and efficiency.

Deep Learning on Point Sets

Properties of Point Sets:

• Unordered: Point clouds lack a specific order, unlike pixel arrays or voxel grids, necessitating network invariance to permutations.
• Interaction among points: Points in a space with a distance metric are not isolated; local structures and interactions among them are significant.
• Invariance under transformations: The learned representation of a point set should remain unchanged under certain transformations, like rotation or translation.

PointNet Architecture:

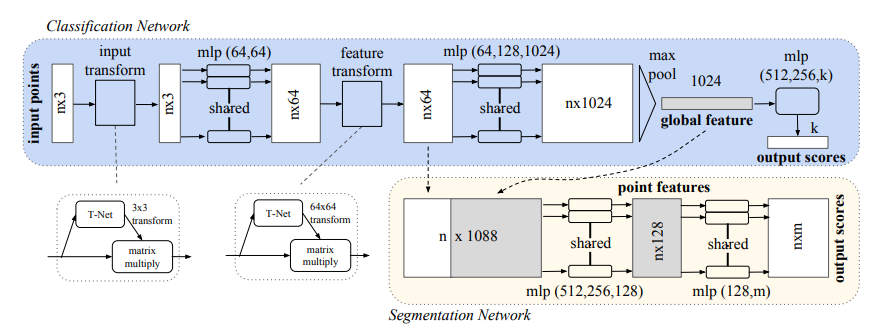
PointNet has a classification network handling n input points for k classes and a segmentation network extending the classification net. The “mlp” (multi-layer perceptron) uses batchnorm for all layers with ReLU, and dropout layers are applied to the final mlp in the classification net.

• Symmetry Function for Unordered Input: PointNet uses a symmetric function to handle unordered point sets, avoiding the challenges of sorting or using Recurrent Neural Networks (RNNs).
• Local and Global Information Aggregation: The architecture includes a max pooling layer for global information and a mechanism for combining global and local knowledge, crucial for tasks like point segmentation.
• Joint Alignment Network: PointNet ensures invariance to geometric transformations by aligning input point sets to a canonical space using an affine transformation matrix. This alignment idea extends to feature space with an added regularization term for stability and better performance.

Theoretical Analysis

Universal Approximation (Theorem 1): The theorem establishes PointNet’s capability to approximate continuous set functions effectively. By ensuring continuity, small perturbations to the input point set are shown not to drastically change function values, such as those used in classification or segmentation tasks. The theorem suggests that PointNet can arbitrarily approximate continuous set functions with a sufficiently large number of neurons in the max pooling layer.

Bottleneck Dimension and Stability (Theorem 2): This part delves into the expressiveness of PointNet and its sensitivity to the dimension (K) of the max pooling layer. The theorem demonstrates that the network is robust to small corruptions or extra noise points in the input set. Specifically, it establishes that the output of the network is not likely to change significantly in the presence of such perturbations. The concept of “bottleneck dimension” (K) is introduced, emphasizing that the output is determined by a finite subset of points (CS) within the input set.

Implications and Robustness: The implications of Theorem 2 are discussed, highlighting that the output remains unchanged up to input corruption if the critical point set (CS) is preserved. The concept of the bottleneck dimension (K) further explains the robustness of the model to point perturbations, corruption, and extra noise points. The robustness is attributed to the network’s ability to summarize a shape by focusing on a sparse set of key points, akin to the sparsity principle in machine learning models. Experimental evidence suggests that these key points effectively form the skeleton of an object.

Application to Classification (Table 1): Theoretical insights are correlated with experimental results in the context of 3D object classification on the ModelNet40 dataset. PointNet achieves state-of-the-art performance among deep networks on 3D input, demonstrating its effectiveness in practical applications.

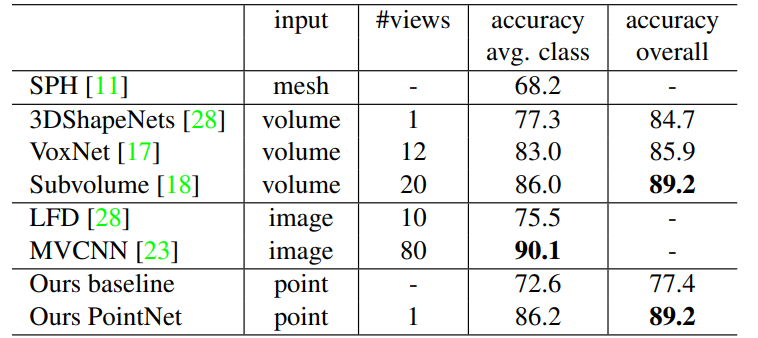
Table 1. Classification results on ModelNet40.

In summary, the theoretical analysis provides a foundation for understanding PointNet’s capabilities, including its universal approximation ability and robustness to input variations. Experimental results validate these theoretical insights, showcasing PointNet’s strength in 3D object classification and its ability to learn meaningful representations from sparse key points.

Experiment

Applications:

The experiments are categorized into four parts. The first part demonstrates the applicability of PointNets to various 3D recognition tasks, including object classification, object part segmentation, and semantic scene segmentation. PointNets outperform previous methods on benchmarks for these tasks, showcasing their effectiveness.

• 3D Object Classification (Table 1):
  • PointNets achieve state-of-the-art performance on the ModelNet40 shape classification benchmark.
  • The network’s simplicity, with fully connected layers and max pooling, leads to superior inference speed and parallelization capabilities.

• 3D Object Part Segmentation (Table 2):

  

Table 2. Segmentation results on ShapeNet part dataset

• PointNets are applied to fine-grained 3D object part segmentation, outperforming traditional methods.
• Results on ShapeNet part dataset demonstrate improved mean Intersection over Union (mIoU) compared to baseline methods.

• The network shows robustness to partial scans and maintains reasonable predictions.

• Semantic Segmentation in Scenes (Table 3):

  

  Table 3. Results on semantic segmentation in scenes.

  • PointNets are extended to semantic scene segmentation, achieving significant performance improvement over a baseline using handcrafted features.
  • A subsequent 3D object detection system based on semantic segmentation outperforms a previous state-of-the-art method.

Architecture Design Analysis:

This section validates design choices through control experiments and explores the effects of network hyperparameters.

• Comparison with Alternative Order-invariant Methods:
  • PointNets’ order-invariant design, utilizing max pooling, is compared with alternative methods such as multi-layer perceptrons (MLP) on sorted and unsorted points. Max pooling demonstrates superior performance, validating PointNets’ approach.

• Effectiveness of Input and Feature Transformations (Table 5):

  

  Table 5. Effects of input feature transforms.

  • Input and feature transformations contribute positively to classification accuracy.
  • Combining both transformations and regularization achieves the best performance.

• Robustness Test (Fig. 6):

  

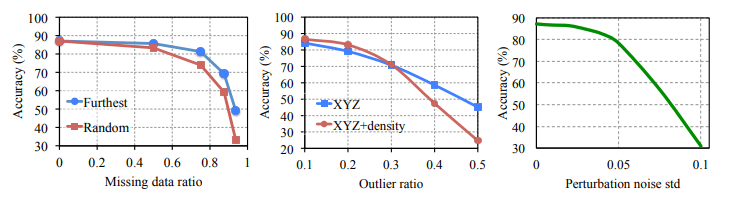
  Figure 6. PointNet robustness test.

  • PointNets exhibit robustness to various input corruptions, including point deletions, insertions, and perturbations.

Visualizing PointNet:

Visualization of critical point sets (CS) and upper-bound shapes (NS) illustrates how PointNets summarize the skeleton of shapes. CS captures key points, while NS reflects the largest possible point cloud providing the same global shape feature.

Time and Space Complexity Analysis (Table 6):

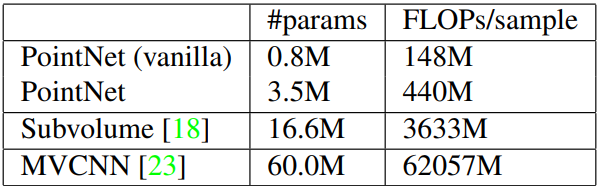
Table 6. Time and space complexity of deep architectures for 3D data classification.

PointNets demonstrate efficiency in both space and time complexity compared to volumetric and multi-view-based architectures. They are orders of magnitude more efficient in terms of computational cost and parameters, showcasing scalability and potential for real-time applications.

In summary, the experiments validate the effectiveness, robustness, and efficiency of PointNets across various 3D recognition tasks, making them a promising approach for real-world applications.

Conclusion

In conclusion, they introduced PointNet, an innovative deep neural network for processing point clouds. It provides a unified solution for various 3D recognition tasks, outperforming or matching state-of-the-art results on standard benchmarks. The work includes theoretical analysis and visualizations to enhance their understanding of the network.

This is just a summary from my point of view for more details please find the original paper here.